Sometimes you are assigned the task to import legacy data and one of the datatypes is FLOAT (or REAL). Then you can use my SQLCLR function that decodes all values to proper decimal representation.
Here is an explanation of how you decode IEEE754 binary value to it’s decimal representation.
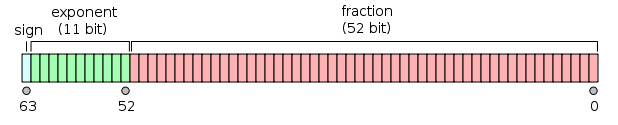
IEEE-754 is stored in three parts.
For FLOAT, IEEE-754 uses 1 bit for the sign, 11 bits for the exponent, and 52 bits for the fraction.
REAL uses 1 bit for the sign, 8 bits for the exponent, and 23 bits for the mantissa.
In this example we till use the binary value of 0x3E200000, as seen above.
For the exponent, you can apply normal bit calculation and get the value to 124 (01111100 binary is 124 decimal).
However, the exponent is biased with 127 for REAL and 1023 for FLOAT. Subtract 127 from 124 and you get -3. The exponent is then worth 2^-3 which is 0.125.
For the fraction, each bit is valued at 1 / (2^bit) such as
1/2 (2^1) = 0.5
1/4 (2^2) = 0.25
1/8 (2^3) = 0.125
1/16 (2^4) = 0.0625
1/32 (2^5) = 0.03125
1/64 (2^6) = 0.015625
1/128 (2^7) = 0.0078125
1/256 (2^8) = 0.00390625
1/512 (2^9) = 0.001953125
1/1024 (2^10) = 0.0009765625
1/2048 (2^11) = 0.00048828125
1/4096 (2^12) = 0.000244140625
1/8192 (2^13) = 0.0001220703125
1/16384 (2^14) = 0.00006103515625
1/32768 (2^15) = 0.000030517578125
1/65536 (2^16) = 0.0000152587890625
1/131072 (2^17) = 0.00000762939453125
1/262144 (2^18) = 0.000003814697265625
1/524288 (2^19) = 0.0000019073486328125
1/1048576 (2^20) = 0.00000095367431640625
1/2097152 (2^21) = 0.000000476837158203125
1/4194304 (2^22) = 0.0000002384185791015625
1/8388608 (2^23) = 0.00000011920928955078125
The fraction part is summed up to 0.25. Now you multiply 0.125 with 0.25 to get 0.03125. This value is then added to the exponent 0.125 to get the fraction representation of 0.15625.
Let us try the binary value of 0x415984B6 and see which decimal value that is converted to. Hex 0x415984B6 is binary 01000001010110011000010010110110. The sign is 0, the exponent is 10000010 and the fraction is 10110011000010010110110.
In decimal, the fraction is 130 but remember this value is biased with 127 so the exponent value is 2^3, which is 8.
The fraction part is 0.6993625164031982421875 in decimal. Multiply 0.6993625164031982421875 with 8 to get 5.5949001312255859375 and then add the exponent 8. This value of 13.5949001312255859375 is the actual decimal representation the the REAL value 13.5949 that was stored in the column in the first place. For FLOAT, the value of 13.5949 is 0x402B3096BB98C7E3, which is 13.5949000000000008725464795134030282497406005859375 in decimal.
On some CPUs! On other CPU it might be 13.594899999999999096189640113152563571929931640625.
It depends on how the CPU is storing the IEEE754 value. In some cases it choses is the nearest under, in some cases it choses the nearest over and in some cases, it choses the nearest under value or nearest over value that has the smallest difference from the original value.
We also have to remember that IEEE-754 also holds special values such as NaN, Infiinty and so on. So we also have to check for those special values, and we do that by checking the exponent. If the exponent is decimal 255 for REAL, the number is not valid.
Easiest is the start with the sign, multiply with the fraction part and then multiply with the exponent part.
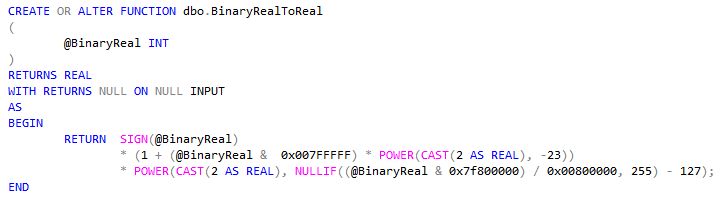
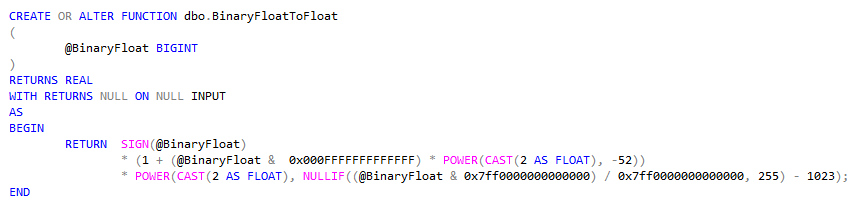
See how I handle the 8 bits for the exponent (0x7f8) and the 23 bits for the fraction (0x007FFFFF)? When applying the same logic for FLOAT, the function look like this.
These two IEEE-754 representations are usually named binary32 (real) and binary64 (float). There are also binary16, binary128 and binary256.
Binary16 uses 5 bits for the exponent and 10 bits for the fraction, binary128 uses 15 bits for the exponent and 112 bits for the fraction and binary256 that uses 19 bits for the exponent and 236 bits for the fraction.
We can use the same logic as written in the two functions above, but there is no compatible datatype in SQL Server that can store the value properly.
But sometimes you only need a human readable represenation of the stored float value and this is one fast way to accomplish that.
You can call this algorithm a nice way to compensate for the “nearest under approximation” binary value.
DECLARE @Sample TABLE
(
f FLOAT NOT NULL
);
INSERT @Sample
(
f
)
VALUES (-13.5949),
(-13.5948),
(13.5948),
(13.5949);
SELECT f,
CAST(f AS DECIMAL(37, 19)),
ROUND(CAST(f AS DECIMAL(34, 17)) + POWER(CAST(SIGN(f) AS DECIMAL(1, 0)) * CAST(10 AS DECIMAL(34, 17)), FLOOR(LOG10(ABS(f))) – 16), 15 – FLOOR(LOG10(ABS(f)))) AS [Human readable]
FROM @Sample;
And at last some statistics about FLOAT and exact storage