Prime numbers. Who doesn’t love them? They have a special place in mathemathics and also very useful in many areas, especially in cryptography.
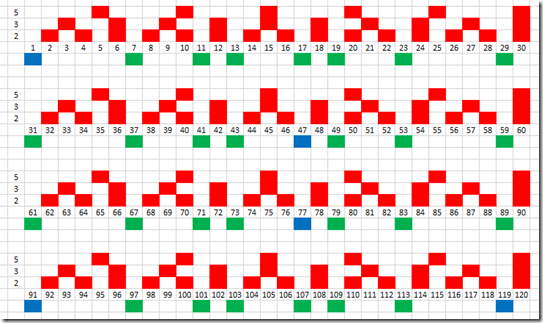
Since I know there are some repetitive patterns about primes, I started out writing all numbers from 1 to 120 on a paper.
I segmented the number in partitions of 30 because the first 3 prime numbers 2, 3 and 5 have a product of 30, and this pattern repeat itself since no other prime can have 2, 3, or 5 as a factor.
As you can see in the image above, the red blocks are the numbers that are definately not a prime number. Left are the green and blue numbers that are possible prime numbers candidates. As you can see, there are now only 8 candidates in each partition. In reality there are only 7 since at least one possible prime number candidate is false.
1 is per definition not a prime number, 47 is the product of 7 and 7, 77 is the product of 7 and 11, 91 is the product of 7 and 13, and last 119 is the product of 7 and 17. With this information, I only have to test 8 of 30 numbers in each partition, ie only 26.67% of the numbers, a significant improvement.
I decided that creating a certain number of partitions up to the wanted prime number should be enough. Further, I don’t have to check 2, 3, and 5 because these numbers already have been used to set the partition size (named x).
The first number I have to check is 7 (x – 23). The following numbers are 11 (x – 19), 13 (x – 17), 17 (x – 13), 19 (x- 11), 23 (x – 7) and 29 (x – 1).
But since I have offset the sequence by seven numbers I have have to include 31 (x + 1). Now I have all my prime number candicates and I save these in a temporary table. If I for example want to display all prime numbers up to 1 000 000, I only have to store 266 672 prime numbers candidates.
Now when I have all my prime number candidates, all I have to do is to check of there exists a prime number as a factor of the larger prime number candidate. And it is common knownledge you ony have to check for a factor up to the size of square root of the largets prime number.
This is the final code to produce prime numbers very fast.
CREATE TABLE #Numbers
(
PrimeCandidate INT NOT NULL,
PrimalityTest BIGINT PRIMARY KEY CLUSTERED
);
DECLARE @MaxPrime BIGINT = 1000000;
WITH n0(p)
AS (
SELECT 1 UNION ALL
SELECT 1
), n1(p)
AS (
SELECT 1
FROM n0 AS a
CROSS JOIN n0 AS b
), n2(p)
AS (
SELECT 1
FROM n1 AS a
CROSS JOIN n1 AS b
), n3(p)
AS (
SELECT 1
FROM n2 AS a
CROSS JOIN n2 AS b
), n4(p)
AS (
SELECT 1
FROM n3 AS a
CROSS JOIN n3 AS b
), n5(p)
AS (
SELECT 1
FROM n4 AS a
CROSS JOIN n4 AS b
)
INSERT #Numbers
(
PrimeCandidate,
PrimalityTest
)
SELECT f.PrimeCandidate,
f.PrimeCandidate * f.PrimeCandidate AS PrimalityTest
FROM (
SELECT TOP (1 + @MaxPrime / 30)
30 * ROW_NUMBER() OVER (ORDER BY p) AS Segment
FROM n5
) AS v(Segment)
CROSS APPLY (
VALUES (v.Segment – 23),
(v.Segment – 19),
(v.Segment – 17),
(v.Segment – 13),
(v.Segment – 11),
(v.Segment – 7),
(v.Segment – 1),
(v.Segment + 1)
) AS f(PrimeCandidate)
WHERE f.PrimeCandidate <= @MaxPrime;
SELECT Prime
FROM (
VALUES (2),
(3),
(5)
) AS v(Prime)
WHERE Prime <= @MaxPrime
UNION ALL
SELECT n.PrimeCandidate AS Prime
FROM #Numbers AS n
WHERE NOT EXISTS (
SELECT *
FROM #Numbers AS p
WHERE p.PrimalityTest <= n.PrimeCandidate
AND n.PrimeCandidate % p.PrimeCandidate = 0
);
DROP TABLE #Numbers;
This algorithm produces all prime numbers (78 498) up to 1 000 000 in less than 1.5 seconds on my laptop. I have tried to include 7 as base prime number to increase the partition size to 210, but the 48 prime number candidates (22.86%) didn’t improve the performance much.
CREATE TABLE #Numbers
(
PrimeCandidate INT NOT NULL,
PrimalityTest BIGINT PRIMARY KEY CLUSTERED
);
DECLARE @MaxPrime BIGINT = 1000000;
WITH n0(p)
AS (
SELECT 1 UNION ALL
SELECT 1
), n1(p)
AS (
SELECT 1
FROM n0 AS a
CROSS JOIN n0 AS b
), n2(p)
AS (
SELECT 1
FROM n1 AS a
CROSS JOIN n1 AS b
), n3(p)
AS (
SELECT 1
FROM n2 AS a
CROSS JOIN n2 AS b
), n4(p)
AS (
SELECT 1
FROM n3 AS a
CROSS JOIN n3 AS b
), n5(p)
AS (
SELECT 1
FROM n4 AS a
CROSS JOIN n4 AS b
)
INSERT #Numbers
(
PrimeCandidate,
PrimalityTest
)
SELECT f.PrimeCandidate,
f.PrimeCandidate * f.PrimeCandidate AS PrimalityTest
FROM (
SELECT TOP (1 + @MaxPrime / 210)
210 * ROW_NUMBER() OVER (ORDER BY p) AS Segment
FROM n5
) AS v(Segment)
CROSS APPLY (
VALUES (v.Segment – 199),
(v.Segment – 197),
(v.Segment – 193),
(v.Segment – 191),
(v.Segment – 187),
(v.Segment – 181),
(v.Segment – 179),
(v.Segment – 173),
(v.Segment – 169),
(v.Segment – 167),
(v.Segment – 163),
(v.Segment – 157),
(v.Segment – 151),
(v.Segment – 149),
(v.Segment – 143),
(v.Segment – 139),
(v.Segment – 137),
(v.Segment – 131),
(v.Segment – 127),
(v.Segment – 121),
(v.Segment – 113),
(v.Segment – 109),
(v.Segment – 107),
(v.Segment – 103),
(v.Segment – 101),
(v.Segment – 97),
(v.Segment – 89),
(v.Segment – 83),
(v.Segment – 79),
(v.Segment – 73),
(v.Segment – 71),
(v.Segment – 67),
(v.Segment – 61),
(v.Segment – 59),
(v.Segment – 53),
(v.Segment – 47),
(v.Segment – 43),
(v.Segment – 41),
(v.Segment – 37),
(v.Segment – 31),
(v.Segment – 29),
(v.Segment – 23),
(v.Segment – 19),
(v.Segment – 17),
(v.Segment – 13),
(v.Segment – 11),
(v.Segment – 1),
(v.Segment + 1)
) AS f(PrimeCandidate)
WHERE f.PrimeCandidate <= @MaxPrime;
SELECT Prime
FROM (
VALUES (2),
(3),
(5),
(7)
) AS v(Prime)
WHERE Prime <= @MaxPrime
UNION ALL
SELECT n.PrimeCandidate AS Prime
FROM #Numbers AS n
WHERE NOT EXISTS (
SELECT *
FROM #Numbers AS p
WHERE p.PrimalityTest <= n.PrimeCandidate
AND n.PrimeCandidate % p.PrimeCandidate = 0
);
DROP TABLE #Numbers;